三角形覆盖正方形的研究

命题

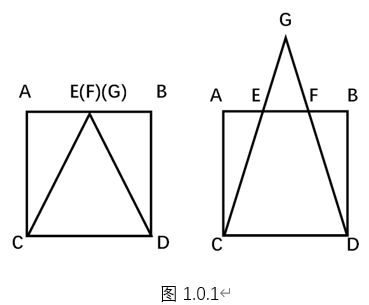
如图 1.0.1，等腰三角形 GCD 与正方形 ABCD 共边 CD；CG、DG 分别交 AB 于点 E、点 F. 则问不断增加等腰三角形 GCD 的高，能否使等腰三角形 GCD 完全覆盖住正方形 ABCD？

证明 / 证伪

设正方形边长为 a，三角形 GCD 的高为 x，四边形 EFCD 的面积为 y

方法一

\because ABCD\text{是正方形} \\ \therefore \angle A=\angle B=90\degree\text{，}AB\bot AC\text{于点}A\text{且}\bot BD\text{于点}B\text{，}AB\text{//}CD \\ \therefore \bigtriangleup AEC\text{与}\bigtriangleup BFD\text{都是直角三角形，其中}∠A=∠B=90\degree\text{，且}\bigtriangleup GCD\text{∼}\bigtriangleup GEF \\ \text{又}\because \text{三角形}GEF\text{的高是}\left( x-a \right) \text{，三角形}GCD\text{的高是}x \\ \therefore EF:CD=\left( x-a \right) :x \\ \therefore \mathrm{EF}=\mathrm{CD}\frac{x-a}{x}=\frac{a\left( x-a \right)}{x}=\frac{ax-a^2}{x}=a-\frac{a^2}{x} \\ \therefore AE=BF=\frac{1}{2}\left( AB-EF \right) =\frac{1}{2}\left[ a-\left( a-\frac{a^2}{x} \right) \right] =\frac{a^2}{2x} \\ \therefore \tan \angle BDF=\tan \angle ACE=\frac{AE}{AC}=\frac{BF}{BD}=\frac{\frac{a^2}{2x}}{a} \\ \text{当}\bigtriangleup GCD\text{完全覆盖正方形}ABCD\text{时，有}∠GDC=∠GCD\geqslant 90\degree \\ \text{当}∠GDC=∠GCD=90\degree\text{时，} \\ \tan ∠BDF=\tan \left( 90\degree-∠GDC \right) =\tan ∠ACE=\tan \left( 90\degree-∠GCD \right) =\tan 0\degree=0 \\ \therefore \frac{AE}{AC}=\frac{BF}{BD}=\frac{\frac{a^2}{2x}}{a}=0 \\ \therefore \frac{a^2}{2x}=0\text{，}a^2=0\text{，}a=0 \\ \text{此时原式不成立，所以等腰}\bigtriangleup GCD\text{不能完全覆盖住正方形}ABCD \\ \text{当}∠GDC=∠GCD>90\degree\text{时，} \\ \text{有}∠GDC+∠GCD>180\degree \\ \because \text{三角形内角和为}180\degree \\ \therefore \text{此时}GCD\text{不是三角形，不符合题设，所以等腰}\bigtriangleup GCD\text{不能完全覆盖住正方形}ABCD \\ \text{综上所述，等腰}\bigtriangleup GCD\text{不能完全覆盖住正方形}ABCD

方法二

\because ABCD\text{是正方形} \\ \therefore AB//CD \\ \therefore \bigtriangleup GCD\text{∼}\bigtriangleup GEF\text{，四边形}EFCD\text{是梯形} \\ \text{又}\because \bigtriangleup GEF\text{的高是}\left( x-a \right) \text{，}\bigtriangleup GCD\text{的高是}x \\ \therefore EF:CD=\left( x-a \right) :x \\ \therefore \mathrm{EF}=\mathrm{CD}\frac{x-a}{x}=\frac{a\left( x-a \right)}{x}=\frac{ax-a^2}{x}=a-\frac{a^2}{x} \\ \therefore S_{\text{梯形}EFCD}=\frac{1}{2}\mathrm{AC}\left( \mathrm{EF}+\mathrm{CD} \right) =\frac{1}{2}\left[ a\left( a-\frac{a^2}{x} \right) +a \right] =\frac{1}{2}a\left( 2a-\frac{a^2}{x} \right) =a^2-\frac{a^3}{2x} \\ \text{若要让等腰}\bigtriangleup GCD\text{完全覆盖住正方形}ABCD\text{，则显然有}S_{\text{梯形}EFCD}=S_{\text{正方形}ABCD} \\ \text{于是可得}a^2=a^2-\frac{a^3}{2x}\text{，则}\frac{a^3}{2x}=0\text{，故}a^3=0\text{，}a=0 \\ \text{此时原式无意义，所以等腰}\bigtriangleup GCD\text{不能完全覆盖住正方形}ABCD

综上所述，等腰三角形 GCD 无法完全覆盖住正方形 ABCD.

推广

从方法二的证明过程中，可以发现三角形 GCD 可以不是等腰三角形，此时结论依旧成立。所以我们有真命题：在图 1.0.1 中三角形 GCD 无法完全覆盖住正方形 ABCD.

探究

在方法二中，我们得出了正方形 ABCD 的边长 a，三角形 GCD 的高 x 与梯形 EFCD 面积 y 之间的关系式，亦或者说是函数即 $y=\mathrm{a}^2-\frac{\mathrm{a}^3}{2\mathrm{x}}$

那么，若是不让三角形 GCD 完全覆盖正方形 ABCD（不让三角形 GCD 的高等于无限），而是让其高尽量长，趋近于无限呢？

此时，可得 $\underset{x\rightarrow \infty}{\lim}\left( a^2-\frac{a^3}{2x} \right) =a^2$

于是有当三角形 GCD 的高 x 趋近于无限时，梯形 EFCD 的面积趋近于正方形 ABCD 的面积 a², 此时三角形 GCD 在正方形内的面积趋近正方形 ABCD 的面积.

结论

图 1.0.1 中的三角形 GCD 无法完全覆盖住正方形 ABCD，但若三角形 GCD 的高趋近于无限，则此时三角形 GCD 在正方形内的面积趋近正方形 ABCD 的面积.

三角形覆盖正方形的研究

文章摘要

命题

证明 / 证伪

方法一

方法二

推广

探究

结论

目录