学习笔记——二叉树
AI
加载中...
加载中...
二叉树
介绍
- 一种特殊的树形结构,是度数为
2 的树。即二叉树的每个节点最多具有两个子节点,每个节点的字节点分别称为左孩子、右孩子,子树则为左子树,右子树。 - 二叉树可以为空且一定有序。
- 在二叉树的第
i 层上至多有 2i 个节点 (i>=0)。 - 深度为
m 的二叉树上至多有 个节点 (m>=0),一棵深度为 m 且有 个节点的二叉树被称为满二叉树。 - 每一个节点都与深度为
m 的满二叉树中编号为 1~n 的节点一一对应的深度为 m,有 n 个节点的二叉树被称为完全二叉树。 - 对于任意一棵二叉树,若其有
n0 个叶节点,n2 个度为 2 的节点,则一定有 n0=n2+1。 - 具有
n 个节点的完全二叉树的深度是 。 - 在有
n 个节点的完全二叉树中,对于编号为 i 的节点: - 若
,则其无父节点,为根节点,否则其父节点编号为 。 - 若
,则 i 为叶节点,否则其左孩子的编号为 2i。 - 若
,则 i 无右孩子,否则其右孩子的编号为 2i+1。
- 若
如下图即二叉树示意图:
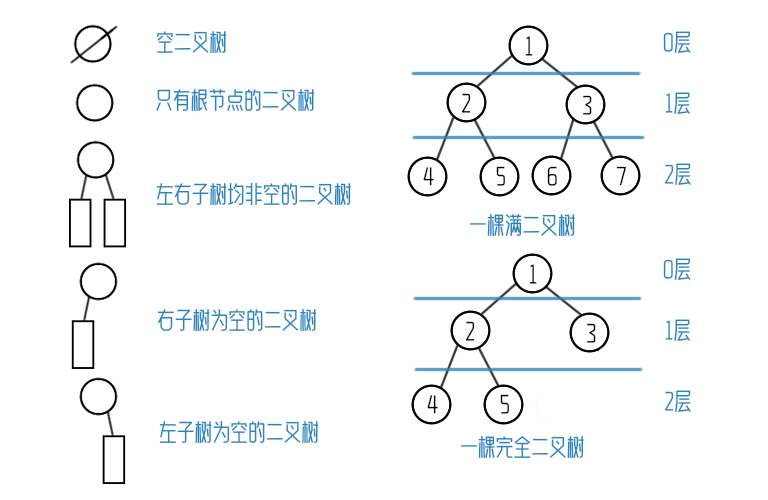
存储结构
单链表结构
1 | |
与树一样,其实就是孩子表示法。
双链表结构
1 | |
同理,其实就是父亲孩子表示法。
遍历
- 先序遍历(输出->
左孩子-> 右孩子) - 中序遍历(左孩子->
输出-> 右孩子) - 后序遍历(左孩子->
右孩子-> 输出)
普通树转二叉树
- 对于每一个节点,去除除最左边的树枝之外的所有树枝。
- 从最左边的节点开始,依次次将同层的每个兄弟节点横向相连。
- 以根节点为中心,将图形顺时针旋转约
45°。
如下图所示:
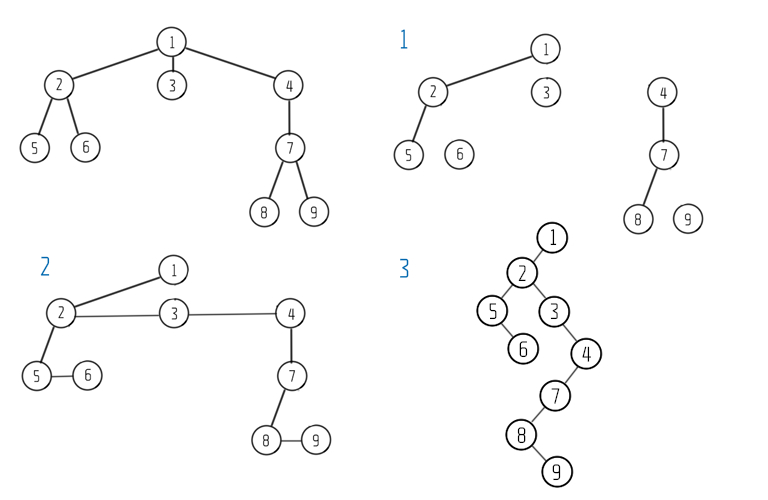
树的计数
具有
题外话
这是第二篇学习笔记,上一篇可以点击这里查看。